Exploring the Lorenz Attractor with PNGwriter
The Lorenz Attractor is a fascinating representation of the behaviour of a particular chaotic system. See the following MathWorld and Wikipedia articles for more information, which explain it very well.
Basically, the equations the following program solves and plots are
|
|
where a = 10, b = 28, c = 8/3.
The system of differential equations was solved using a simple 4th-order Runge-Kutta solver class that I wrote; if there is enough demand I may release it under the GPL. It's incredibly simple, and it's main goal is to be easy to use.
Here are three views of the three-dimensional attractor.
 XY plane |
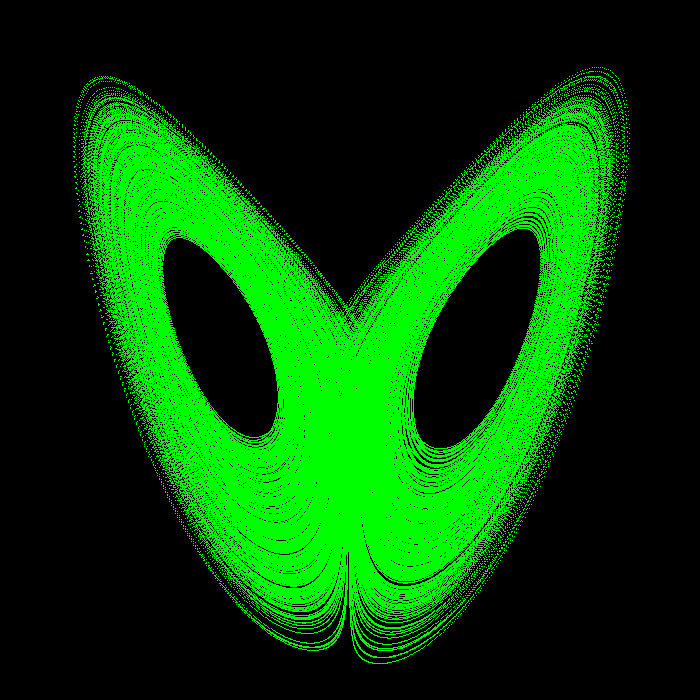 XZ plane |
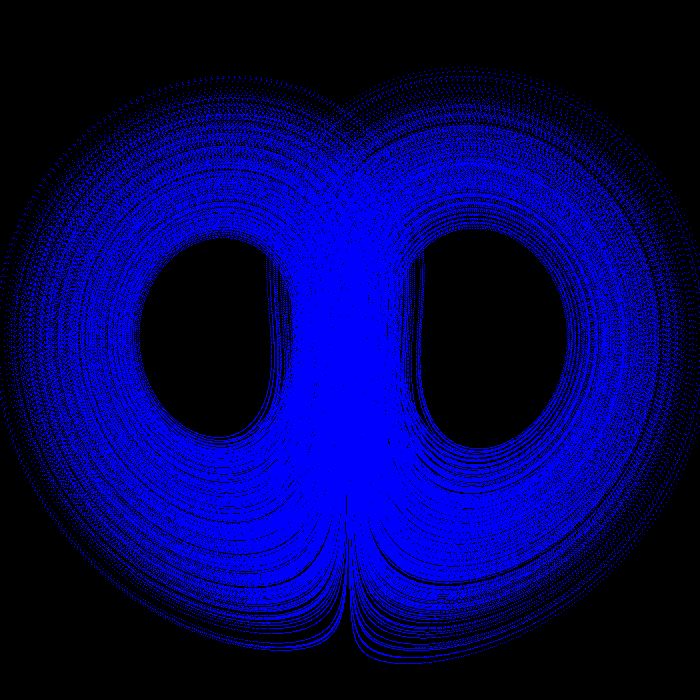 YZ plane |
Here's the code:
// Lorenz Attractor - Test program for PNGwriter
// http://pngwriter.sourceforge.net/
// By Paul Blackburn
#include "rungekutta_3/rungekutta.h"
#include <stdlib.h>
#include <pngwriter.h>
/* Lorenz Equations
* Test program for rungekutta class
* (C) 2004 Paul Blackburn
*
* dX/dt = s*(Y - X)
* dY/dt = r*X - Y - X*Z
* dZ/dt = X*Y - b*Z
*
* args[0] -> s
* args[1] -> r
* args[2] -> b
* args[3] -> X
* args[4] -> Y
* args[5] -> Z
*
* */
double dX(double X, double t, double * args)
{
return args[0]*(args[4] - X);
}
double dY(double Y, double t, double * args)
{
return args[1]*args[3] - Y - args[3]*args[5];
}
double dZ(double Z, double t, double * args)
{
return args[3]*args[4] - args[2]*args[5];
}
int main(int argc, char * argv[])
{
if(argc != 8)
{
std::cout << "Usage: r tmax X0 Y0 Z0 k h." << std::endl;
std::cout << "Suggested values: 22 300 3 3 3 0.5 0.0008 " << std::endl;
return 0;
}
double * args;
args = new double[3];
double X0, Y0, Z0, t0, tmax, h, s, r, b, k, width, height;
width = 700;
height = 700;
t0 = 0.0;
r = atof(argv[1]);
tmax = atof(argv[2]);
X0 = atof(argv[3]);
Y0 = atof(argv[4]);
Z0 = atof(argv[5]);
k = atof(argv[6]);
h = atof(argv[7]);
rungekutta X(&dX, args, X0, t0, h);
rungekutta Y(&dY, args, Y0, t0, h);
rungekutta Z(&dZ, args, Z0, t0, h);
pngwriter xy(width, height, 0, "xy.png");
pngwriter xz(width, height, 0, "xz.png");
pngwriter yz(width, height, 0, "yz.png");
b = 8.0/3.0;
s = 10.0;
args[0] = s;
args[1] = r;
args[2] = b;
for(int i = 0; i < tmax/h; i++)
{
args[3] = X.get_y();
args[4] = Y.get_y();
args[5] = Z.get_y();
xy.plot( (k*width/20.0) * X.iterate_and_get_next_y() + width/2.0,
(k*height/20.0) * Y.iterate_and_get_next_y() + height/2.0,
1.0, 0.0, 0.0);
xz.plot( (k*width/20.0) * X.iterate_and_get_next_y() + width/2.0,
(k*height/20.0) * Z.iterate_and_get_next_y(),
0.0, 1.0, 0.0);
yz.plot( (k*width/20.0) * Y.iterate_and_get_next_y() + width/2.0,
(k*height/20.0) * Z.iterate_and_get_next_y(),
0.0, 0.0, 1.0);
}
xy.close();
xz.close();
yz.close();
delete [] args;
return 0;
}
syntax highlighted by Code2HTML, v. 0.9.1 |
| versión en español | 日本語の ページ |
| home | download | quickstart | examples | manual | forum | legal | links | contacts |
© 2002, 2003, 2004, 2005, 2006, 2007 Paul Blackburn