Explorando el Atractor de Lorenz con PNGwriter
El Atractor de Lorenz es una representación fascinante del comportamiento de un sistema caótico particular. Ver los siguientes artículos de The Lorenz Attractor is a fascinating representation of the behaviour of a particular chaotic system. See the following MathWorld y Wikipedia para más información.
Básicamente, las ecuaciones que el programa soluciona y plotea son
|
|
donde a = 10, b = 28, c = 8/3.
El sistema de ecuaciones diferenciales fue solucionado usando un integrador Ruge-Kutta simple de cuarto orden que escribí; si hay suficiente demanda, podría sacarlo bajo la GPL. Es increíblemente simple, y su principal objetivo es ser fácil de usar.
Aquí hay tres vistas del atractor tridimensional.
 plano XY |
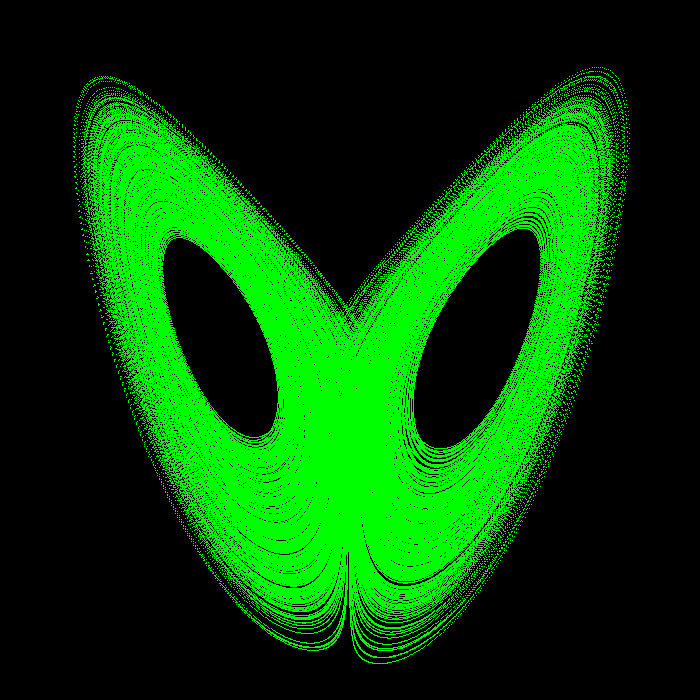 plano XZ |
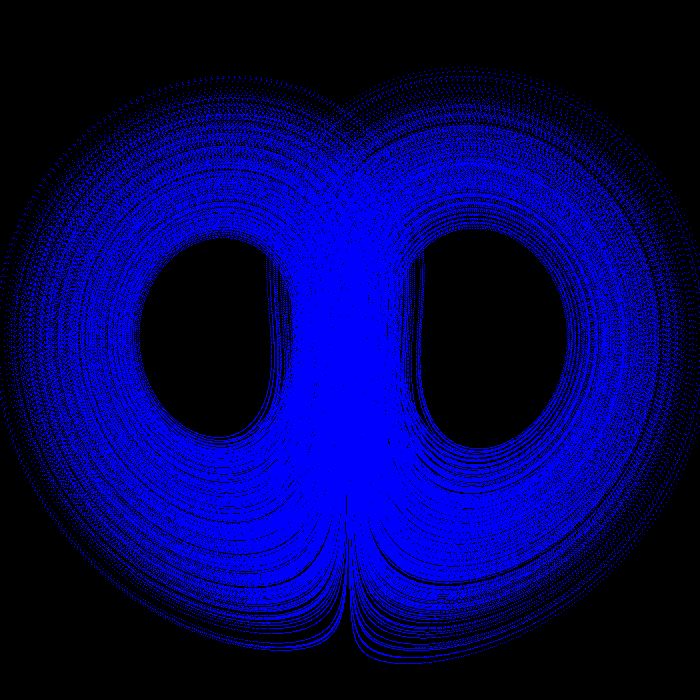 plano YZ |
Aquí está el código:
// Lorenz Attractor - Test program for PNGwriter
// http://pngwriter.sourceforge.net/
// By Paul Blackburn
#include "rungekutta_3/rungekutta.h"
#include <stdlib.h>
#include <pngwriter.h>
/* Lorenz Equations
* Test program for rungekutta class
* (C) 2004 Paul Blackburn
*
* dX/dt = s*(Y - X)
* dY/dt = r*X - Y - X*Z
* dZ/dt = X*Y - b*Z
*
* args[0] -> s
* args[1] -> r
* args[2] -> b
* args[3] -> X
* args[4] -> Y
* args[5] -> Z
*
* */
double dX(double X, double t, double * args)
{
return args[0]*(args[4] - X);
}
double dY(double Y, double t, double * args)
{
return args[1]*args[3] - Y - args[3]*args[5];
}
double dZ(double Z, double t, double * args)
{
return args[3]*args[4] - args[2]*args[5];
}
int main(int argc, char * argv[])
{
if(argc != 8)
{
std::cout << "Usage: r tmax X0 Y0 Z0 k h." << std::endl;
std::cout << "Suggested values: 22 300 3 3 3 0.5 0.0008 " << std::endl;
return 0;
}
double * args;
args = new double[3];
double X0, Y0, Z0, t0, tmax, h, s, r, b, k, width, height;
width = 700;
height = 700;
t0 = 0.0;
r = atof(argv[1]);
tmax = atof(argv[2]);
X0 = atof(argv[3]);
Y0 = atof(argv[4]);
Z0 = atof(argv[5]);
k = atof(argv[6]);
h = atof(argv[7]);
rungekutta X(&dX, args, X0, t0, h);
rungekutta Y(&dY, args, Y0, t0, h);
rungekutta Z(&dZ, args, Z0, t0, h);
pngwriter xy(width, height, 0, "xy.png");
pngwriter xz(width, height, 0, "xz.png");
pngwriter yz(width, height, 0, "yz.png");
b = 8.0/3.0;
s = 10.0;
args[0] = s;
args[1] = r;
args[2] = b;
for(int i = 0; i < tmax/h; i++)
{
args[3] = X.get_y();
args[4] = Y.get_y();
args[5] = Z.get_y();
xy.plot( (k*width/20.0) * X.iterate_and_get_next_y() + width/2.0,
(k*height/20.0) * Y.iterate_and_get_next_y() + height/2.0,
1.0, 0.0, 0.0);
xz.plot( (k*width/20.0) * X.iterate_and_get_next_y() + width/2.0,
(k*height/20.0) * Z.iterate_and_get_next_y(),
0.0, 1.0, 0.0);
yz.plot( (k*width/20.0) * Y.iterate_and_get_next_y() + width/2.0,
(k*height/20.0) * Z.iterate_and_get_next_y(),
0.0, 0.0, 1.0);
}
xy.close();
xz.close();
yz.close();
delete [] args;
return 0;
}
syntax highlighted by Code2HTML, v. 0.9.1 |
| english version | 日本語の ページ |
| página principal | download | comienzo rápido | ejemplos | manual | foro | legal | links | contactos |
© 2002, 2003, 2004, 2005, 2006, 2007 Paul Blackburn